Using bi-LSTM for hmF2 modelling from Ionosondes in the Australian Region
The height of F2 peak (hmF2) is an essential ionospheric parameter and its variations can reflect both the earth magnetic and solar activities. Therefore, reliable prediction of hmF2 is important for the study of space environment, such as solar wind and extreme weather events. However, most current models are unable to forecast the variation of the ionosphere effectively since real-time measurements are required as model inputs. The front image shows the selected ionosonde stations around Australia for hmF2 modelling
In this study, a new Australian regional hmF2 forecast model was developed by using ionosonde measurements and the bidirectional Long Short-Term Memory (bi-LSTM) method. The hmF2 value in the next hour can be predicted using the data in the past five hours at the same location. The inputs chosen from a location of interest include month of the year, local time (LT), Kp, F10.7 and hmF2 as an independent variable vector.
The performance of the new model developed is evaluated by comparing with those from other popular models, such as the AMTB, Shubin, ANN and LSTM models. Results showed that: (1) the new model can substantially outperform all the other four models. (2) Compared to the LSTM model, the new model is proven to be more robust and rapidly convergent. The new model also outperforms that of ANN model by around 30%. (3) the minimum sample number for the bi-LSTM method (i.e. 2000) to converge is about 50% less than that is required for the LSTM method (i.e. 3000). (4) Compared to the Shubin model, the bi-LSTM method can effectively forecast the hmF2 values upto 5 hours. This research is a first attempt in using the deep learning based method for the application of the ionospheric prediction.
hmF2 generation
Three kinds of measurements from ionosonde data are required for the calculation of hmF2: (1) F2 peak plasma frequency (foF2); (2) the ratio of the maximum usable frequency at a distance of 3000 km to the foF2(M(3000)F2); and (3) E peak plasma frequency (foE). The equations are:
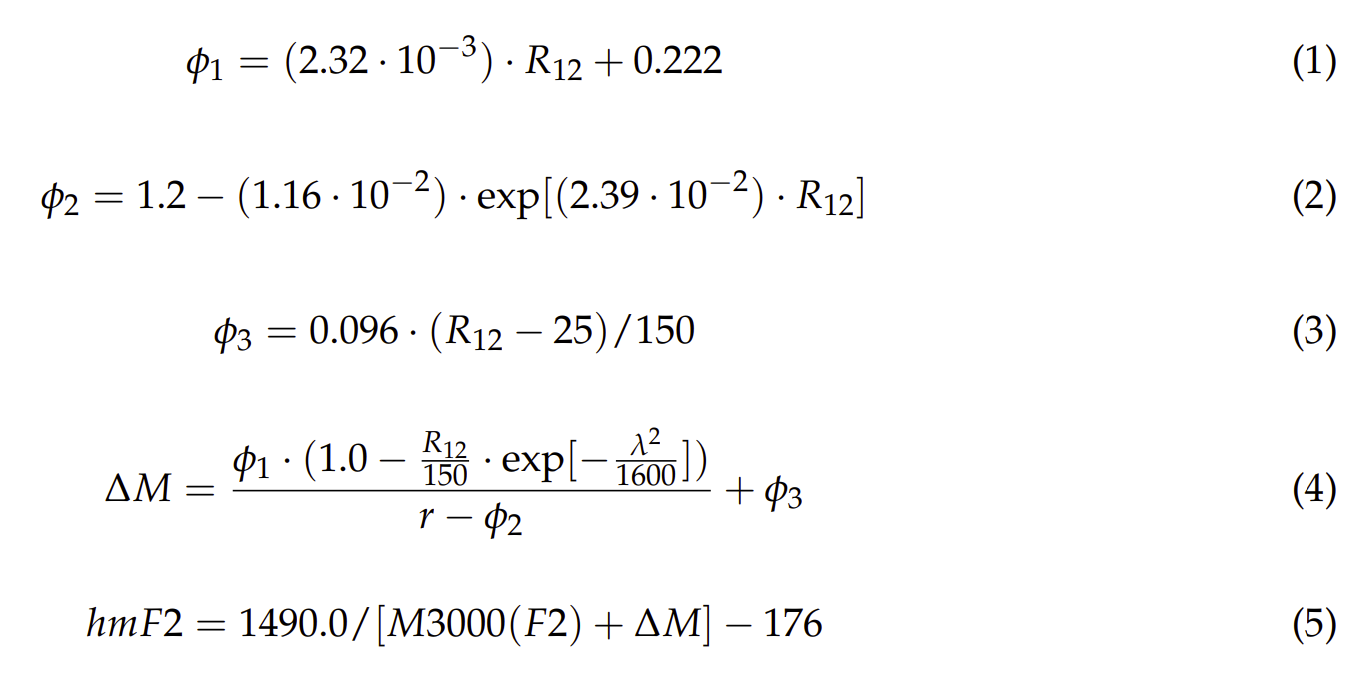
where R12 reflects the strength of solar activity (that can be obtained from https://omniweb.gsfc. nasa.gov/cgi/nx1.cgi), λ is the magnetic dip latitude (that can be obtained from the IGRF-12 model). φ1,2,3 and ∆M are the temporal values during hmF2 calculation, and r = foF2/foE. These equations are also currently used in the IRI model.
Performance
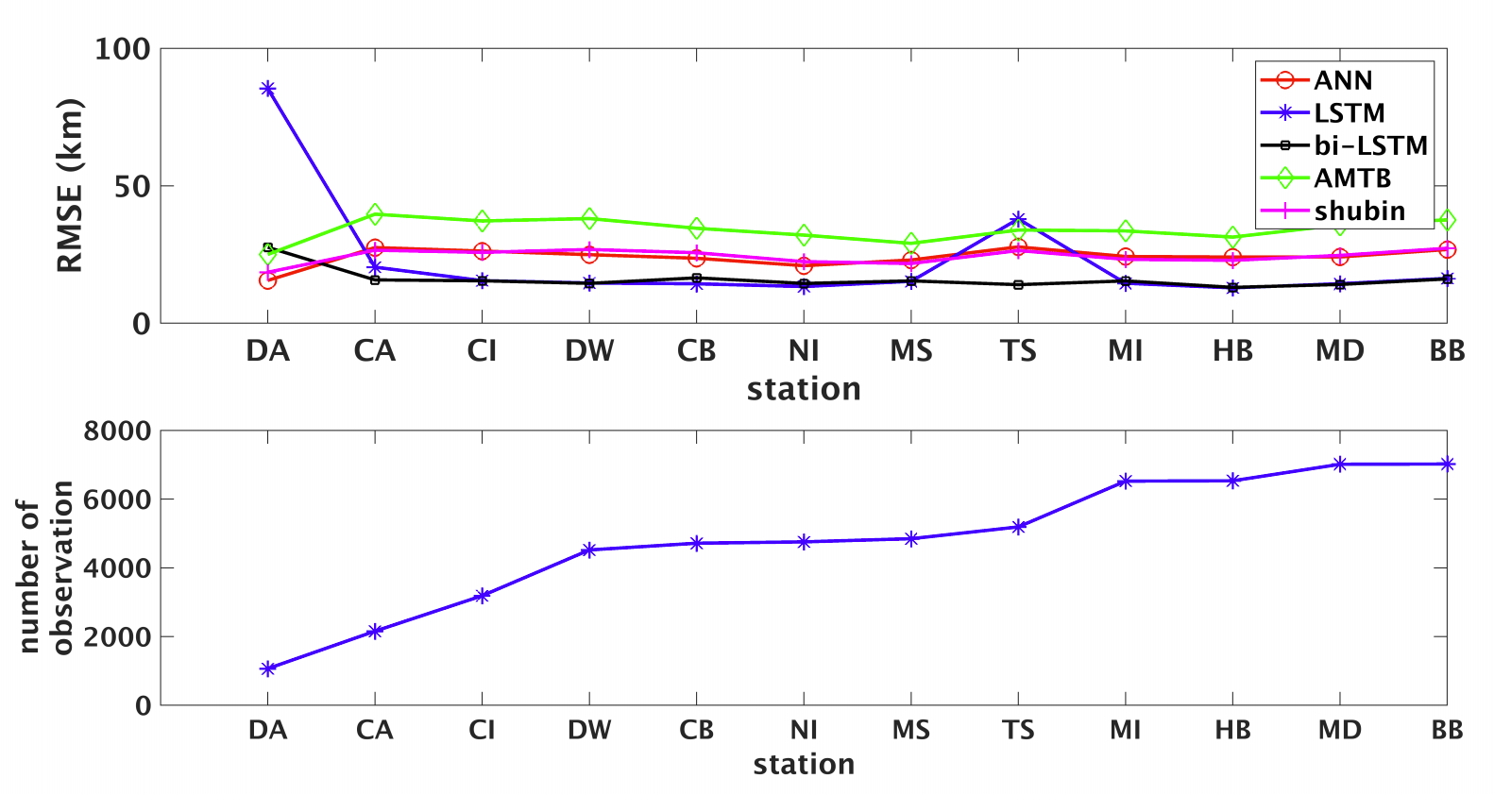
Fig. (a) RMS for each of the five models in each ionosonde station; and (b) number of sample sets in each station.
